Математическая проверка двух кредитов

Я уже дважды писал про то, что если есть два кредита, что ВСЕГДА нужно оплачивать в первую очередь тот, где больше процентная ставка, независимо от суммы кредита.

Последний раз в этой статье. сформулировал тестовый пример:

Первый кредит 600.000 рублей под 12%.

Второй кредит 9.500.000 рублей под 11%.

Куда выгоднее вложить досрочный платеж 1.000 рублей?

Один из моих оппонентов, Влад Орловский из Чикаго, долларовый миллионер, считающий себя хорошо разбирающимся в финансах проверил мои расчеты и показал, что в абсолютных цифрах выгоднее вложить 1.000 досрочного платежа в более объемный кредит.

Он был настолько убедителен, что даже заставил меня сомневаться:

При этом даже нарисовал график некого распределения сумм и ставок, когда досрочный платеж выгоднее вкладывать в более объемный кредит.

Это мнение поддержал наш сорокалетний российский программист 1С из Липецка, в прошлом победитель юношеских математических олимпиад:

Ну и менее успешные в математике читатели тоже поддержали общую волну:

Но были и голоса тех, кто считал, что все-таки выгоднее платить сразу дорогой процент:

Среди них было одно важное мнение, на которое я обратил внимание и задумал когда-нибудь проверить его на практике:

Решил проверить теорию математикой в Google-таблице «Два кредита».

Прежде чем писать эту статью, я подумал о моральной стороне вопроса. Все же Владу Орловскому около 60 лет, он может тяжело перенести своё финансовое фиаско. Ведь он укорял меня в том, что я сразу не мог решить школьную задачу для 9-го класса, а сам не справился с элементарной финансовой задачей. Однако я потому и успешный, что решаю хорошо дорогие, а не дешевые задачи. Ведь в школьной задаче цена ошибки — двойка, а в финансах — впустую потраченные ресурсы. В общем, как бы к этому не отнесся американский старина, истина дороже.

Поэтому хочу вам заверить, что «более дорогой кредит надо гасить ВСЕГДА в первую очередь независимо от объема кредитов«. Ровно то, что я всегда и утверждал.

В чем же была ошибка «голого» расчета Влада и других уважаемых математиков?

Дело в том, что когда мы вносим досрочный платеж на более дорогой кредит, меньший по сумме, его выплаты заканчиваются раньше. В итоге, ежемесячный денежный поток уменьшается, соответственно, сумма выплат получается больше.

Разница при досрочной выплате в 1000 рублей небольшая, всего 1.799 рублей на 60-м месяце (через 5 лет):

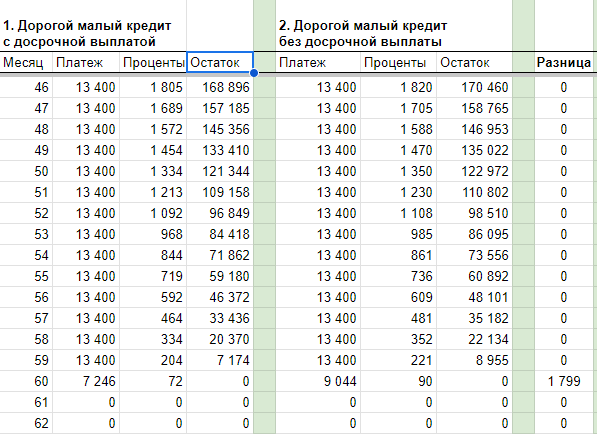
При сумме досрочного платежа в 100.000 рублей разница уже ощутимее 169.118 рублей на 48-м месяце (через 4 года):

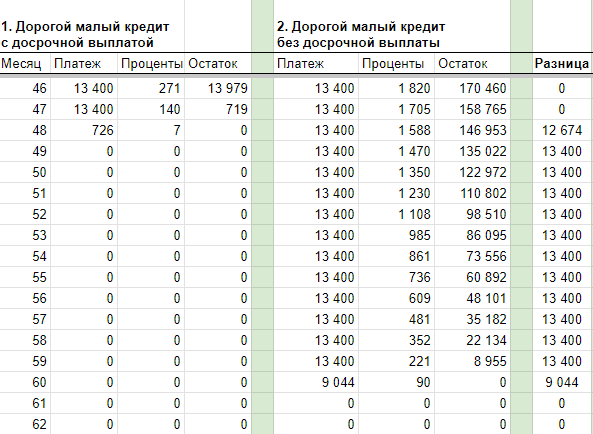
Чтобы сохранить денежный поток в одинаковом объеме, нужно продолжить платежи по первому кредиту по графику, тогда как и ожидалось, досрочная выплата более дорогого кредита ВСЕГДА выгоднее, независимо от объема второго кредита.

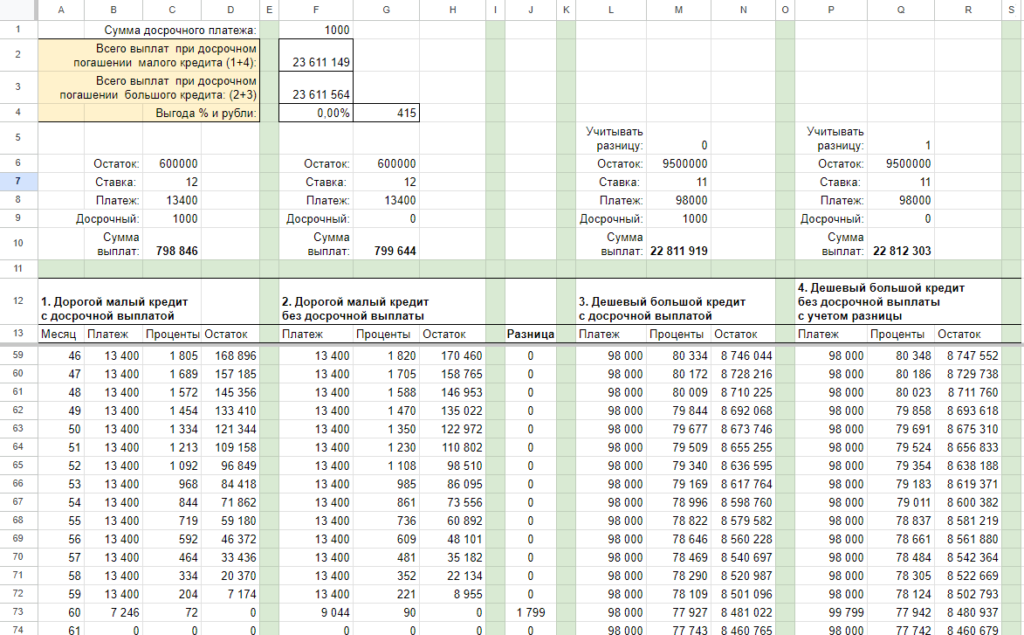
Разница для 1.000 рублей небольшая — 415 рублей:

Разница для 100.000 рублей уже солиднее — 34.358 рублей:

Я надеюсь у Влада будет достаточно мужества, чтобы признать свою ошибку и мою победу. Цифры я предъявил, за «базар» ответил. Буду ждать извинений за «тупицу» и «идиота». Но сам я в эти игры не играю. Люди ошибаются и это нормально. Как показал этот случай, ошибаются даже очень успешные люди, когда ищут желаемый, а не подлинный результат.

Было бы неплохо еще увидеть покаяние Супыря, но на это я не рассчитываю… Мелкий провинциальный человечек…

Вы же можете скопировать Google-таблицу и лично проверить мои выкладки, поиграть с суммами и ставками: